| Název školy: | Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 |
| Autor: | Ing. Marek Nožka |
| Anotace: | Primární a sekundární parametry metalického vedení |
| Vzdělávací oblast: | Informační a komunikační technologie |
| Předmět: | Počítačové sítě a komunikační technika (PSK) |
| Tematická oblast: | Principy přenosu informací |
| Výsledky vzdělávání: | Žák ukazuje rozložení elmag. vlny na vedení |
| Klíčová slova: | metalické vedení, primární a sekundární parametry |
| Druh učebního materiálu: | Online vzdělávací materiál, animace, program |
| Typ vzdělávání: | Střední vzdělávání, 3. ročník, technické lyceum |
| Ověřeno: | VOŠ a SPŠE Olomouc; Třída: 3L |
| Zdroj: | Vlastní poznámky |

Na obrázku je Koaxiální kabel.
Dá se říct, že metalické vedení je elektromagnetické vlny totéž jako optické vlákno pro světlo. To znamená, že vedení vytváří prostředí, kterým se elmag. vlna šíří a do kterého je uzavřena do té míry, že se ohýbá spolu s vedením.
Důležité je pochopit, že vedením se šíří elektromagnetické vlnění. A projevují se zde všechny vlastnosti vln, stejně jako například u zvuku. Každá vlna má svou vlnovou délku, která je dána frekvenci a rychlostí šíření vlny daným prostředím.
$$\lambda = \mathrm{\frac{v}{f} [m; m\cdot s^{-1}, Hz]}$$
Vlnění má jednu velice důležitou vlastnost: Vlnění dokáže přenášet energii.
Podstatou vlnění je kmitání jednotlivých bodů prostředí.
Z pohledu popisu vedení je podstatné v jakém poměru jsou rozměry vedení a vlnová délka vlny.
Při nízkých frekvencích je vlnová délka většinou mnohem větší než jsou rozměry obvodu. V takových případech předpokládáme, že v celém obvodu je v jednom časovém okamžiku stejné napětí a stejný proud

Nenechme se ale zmást pojmem nízká frekvence. Například elektrorozvodná síť používá kmitočet 50 Hz. Tomu odpovídá vlnová délka 6000 km. To je opravdu poměrně dlouhá vlna a proto při řešení běžných střídavých obvodů nemusíme o vlnění nic vědět.
Pokud ale budeme řešit přenos energie z elektrárny do domácnosti, kde se délky vedení pohybují řádově ve stovkách km (To je srovnatelné s délkou vlny), budeme muset počítat s tím, že ve stejném časovém okamžiku je v elektrárně jiné napětí než ve spotřebiči a k celému problému musíme přistupovat zcela jinak -- jako k elektro(magnetickému) vedení.
Pokud je totiž vlnová délka srovnatelná s rozměry obvodu, je v jednom časovém okamžiku v různých částech obvodu různé napětí a různý proud -- tak jak se na dráty natáhne elmag. vlna.

Vedení je tvořeno soustavou dvou vodičů, které ideálně mají po celé délce stejné vlastnosti a konstantní geometrické uspořádání. Také vlastnosti dielektrika, které je v prostoru mezi vodiči se po celé délce nemění.
Pro popis vlastností vedení používáme náhradní schema pro jeden elementární (velmi krátký) úsek vedení.
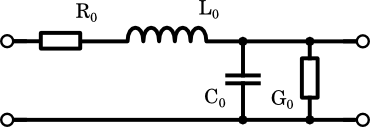
Cele vedení je potom složeno z těchto elementárních úseků, které jsou zapojeny za sebou.

| $\mathrm{R_0 [\Omega \cdot m^{-1}]}$ | odpor vodičů vedení na jednotku délky |
| $\mathrm{L_0 [H \cdot m^{-1}]}$ | indukčnost vodičů vedení na jednotku délky |
| $\mathrm{G_0 [S \cdot m^{-1}]}$ | vodivost mezi oběma vodiči na jednotku délky |
| $\mathrm{C_0 [F \cdot m^{-1}]}$ | kapacita mezi oběma vodiči na jednotku délky |
Primární parametry popisují vedení, ale jsou nevhodné pro praktické výpočty. Proto se zavádí vlnová impedance a konstanta šíření.
Představuje (podle Ohmova zákona) poměr mezi napětí a proudem v každém místě vedení. (Tento pohled je hodně zjednodušený později jej upřesníme.)
$$\mathrm{Z_V = \sqrt{\frac{R_0+j\omega L_0}{G_0+j\omega C_0}}~~~~[\Omega; \Omega, H, S, F] }$$
Konstanta šíření popisuje ztráty v prostředí.
$$\mathrm{\gamma = \sqrt{(R_0+j\omega L_0)(G_0+j\omega C_0)}~~~~[m^{-1}; \Omega, H, S, F]}$$
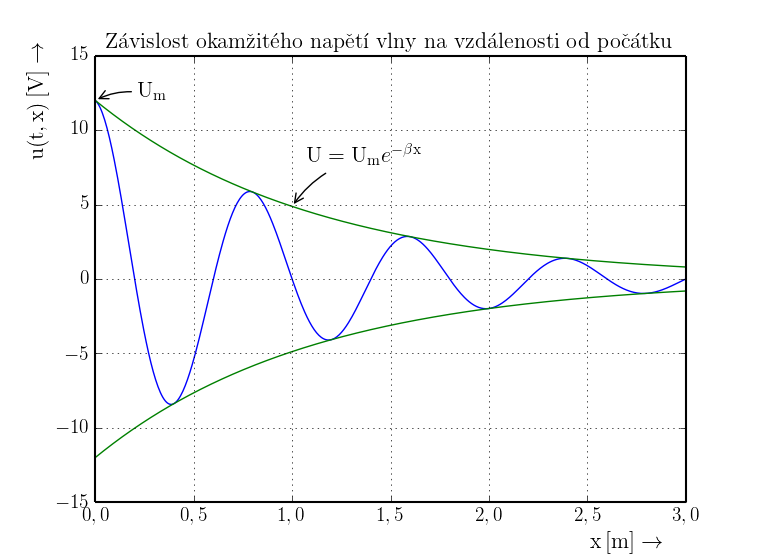
Reálná část konstanty šíření se nazývá měrný útlum $\beta$. Imaginární část se nazývá měrný posuv (fázová konstanta) $\alpha$.
$$\gamma = \beta +j \alpha$$
Měrný útlum $\beta$ popisuje pokles amplitudy vlny v závislosti na vzdálenosti od zdroje.
$$\mathrm{U=U_m}e^{-\beta \mathrm{x}}~~~~[\mathrm{V,V,m^{-1},m}]$$