PSK1-9

Číslicové zpracování signálů

Číslicový signál

Číslicový signál je "pouhá" posloupnost vzorků, tedy posloupnost čísel. V našem příkladu označíme vstupní posloupnost $\mathrm{x}(n)$. $n$ je pořadí vzorku.

x=[ 1, 2, 1.4, 3.1, 1.1, 2, 1, 0, -3.1, -2, -0.9, -2.8, -1.5 ]

Graficky znázornit vstupní posloupnost můžeme takto:

Číslicový filtr, systém

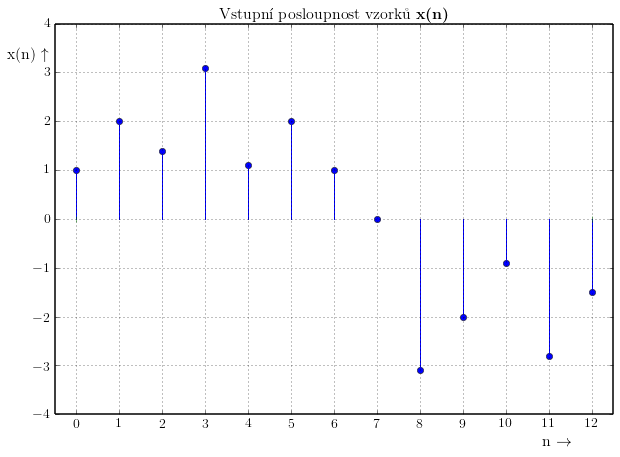
Filtr obecně slouží ke změně časového průběhu nebo frekvenčního spektra signálu. Číslicovým filtr pracuje na následujícím principu: Filtr bere vstupní vzorky, jednotlivé vzorky váhuje (vynásobí je příslušnou konstantou) a sečte je. Výsledkem je výstupní posloupnost $\mathrm{y}(n)$.

Příslušné konstanty -- váhy jednoznačně určují vlastnosti filtru a jejich velikost je předmětem návrhu filtru.

Obecné schéma číslicového filtru vidíme na následujícím obrázku. (Schéma je zjednodušené a nezahrnuje zpětné vazby.)

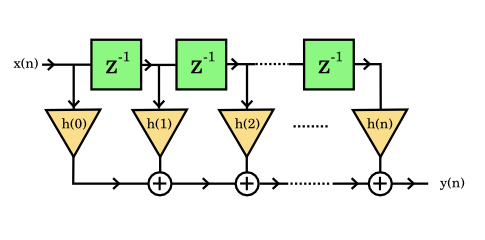
$\mathrm{z}^{-1}$ označuje zpoždění o jeden vzorek (jeden takt). To znamená, že číslicový systém musí mít paměť a pracovat nejen s aktuálním vzorkem, ale i s několika vzorky předešlými.

$\mathrm{h}(n)$ označuje konstantu (váhu), kterou je příslušný vstupní vzorek vynásoben. Právě tyto váhy příslušný filtr (systém) jednoznačně charakterizují a určují jeho chování. Říkáme jim impulzní charakteristika $\mathrm{h}(n)$.

Impulzní charakteristika

Impulzní charakteristika $\mathrm{h}(n)$ je obecně odezva na tzv. jednotkový impulz. Jednotkový impulz je jediný vzorek o hodnotě jedna.

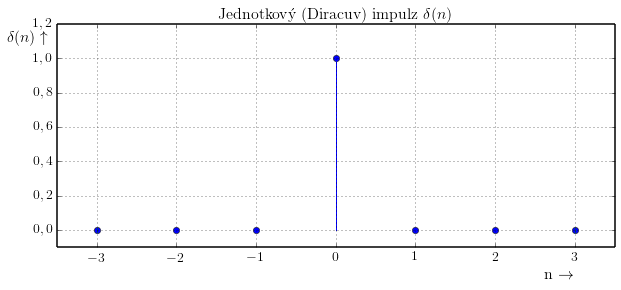
Mějme následující filtr:

h(n) = [ 0.1, 0.2, 0.5, 0.3 ]

... jeho vnitřní uspořádání, by se dalo nakreslit asi takto:

Jestliže přivedeme na vstup tohoto systému jednotkový impulz

tedy $\mathrm{x}(n)=\mathrm{\delta}(n)$

potom na výstupu dostáváme impulzní charakteristiku

tedy $\mathrm{y}(n)=\mathrm{h}(n)$

• v okamžiku $n=0$ se uplatní pouze váha $\mathrm{h}(0)=0.1$
• v okamžiku $n=1$ se uplatní pouze váha $\mathrm{h}(1)=0.2$
• v okamžiku $n=2$ se uplatní pouze váha $\mathrm{h}(2)=0.5$
• v okamžiku $n=3$ se uplatní pouze váha $\mathrm{h}(3)=0.3$

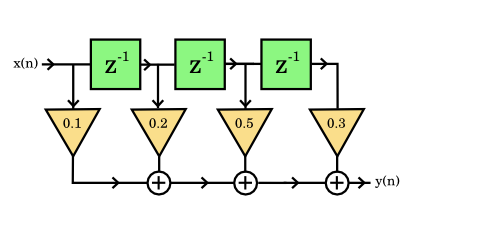
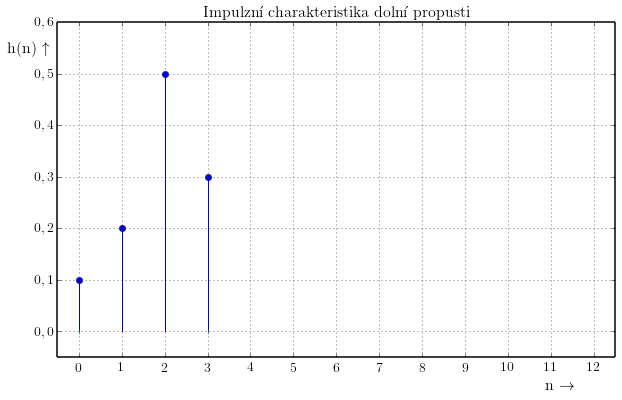
(Ostatní váhy jsou vždy násobeny nulou.)

Průchod signálu filtrem

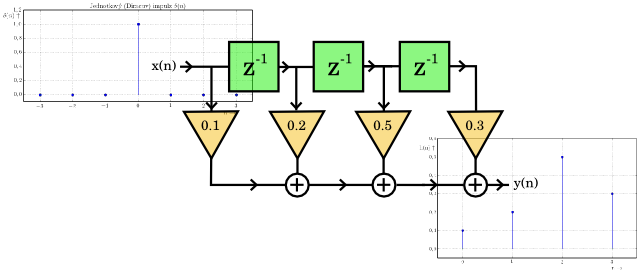
Nyní přivedeme na vstup filtru posloupnost $\mathrm{x}(n)$.

x=[ 1, 2, 1.4, 3.1, 1.1, 2, 1, 0, -3.1, -2, -0.9, -2.8, -1.5 ]

Průchod filtru můžeme znázornit následujícím způsobem: Dáme pod sebe vstupní posloupnost $\mathrm{x}(n)$ a časově převrácenou impulzní charakteristiku $\mathrm{h}(n)$ a budeme násobit vždy vzorky, které jsou pod sebou. (Toto odpovídá matematické operaci konvoluce).

krok $\mathrm{n}=0$

$\mathrm{y}(0)=0.1 \cdot 1 + 0.2 \cdot 0 + 0.5 \cdot 0 + 0.3 \cdot 0 = 0.1$

krok $\mathrm{n}=1$

$\mathrm{y}(1)=0.1 \cdot 2 + 0.2 \cdot 1 + 0.5 \cdot 0 + 0.3 \cdot 0 = 0.4$

krok $\mathrm{n}=2$

$\mathrm{y}(2)=0.1 \cdot 1.4 + 0.2 \cdot 2 + 0.5 \cdot 1 + 0.3 \cdot 0 = 1.04$

krok $\mathrm{n}=3$

$\mathrm{y}(3)=0.1 \cdot 3.1 + 0.2 \cdot 1.4 + 0.5 \cdot 2 + 0.3 \cdot 1 = 1.89$

krok $\mathrm{n}=4$

$\mathrm{y}(4)=0.1 \cdot 1.1 + 0.2 \cdot 3.1 + 0.5 \cdot 1.4 + 0.3 \cdot 2 = 2.03$

krok $\mathrm{n}=5$

$\mathrm{y}(5)=0.1 \cdot 2 + 0.2 \cdot 1.1 + 0.5 \cdot 3.1 + 0.3 \cdot 1.4 = 3.29$

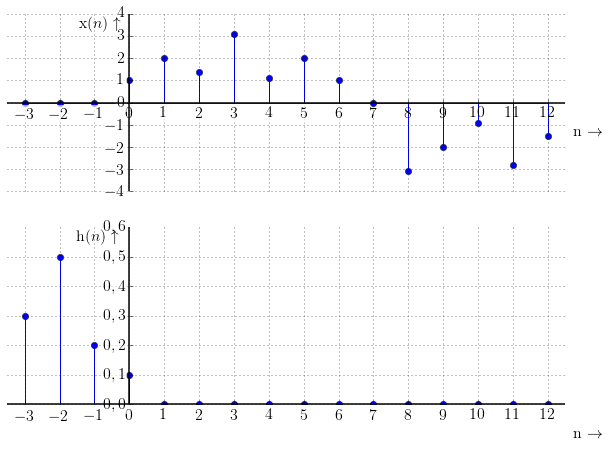
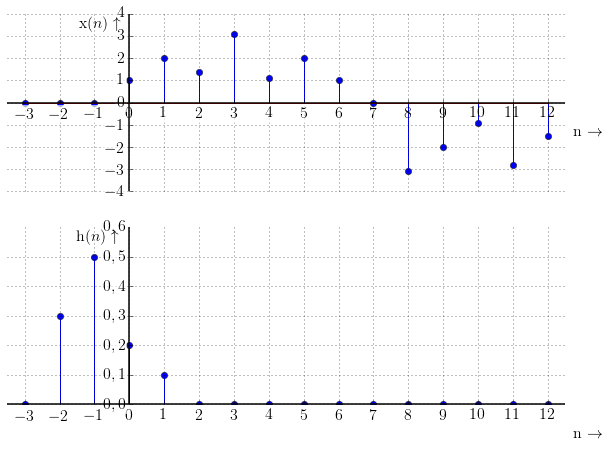
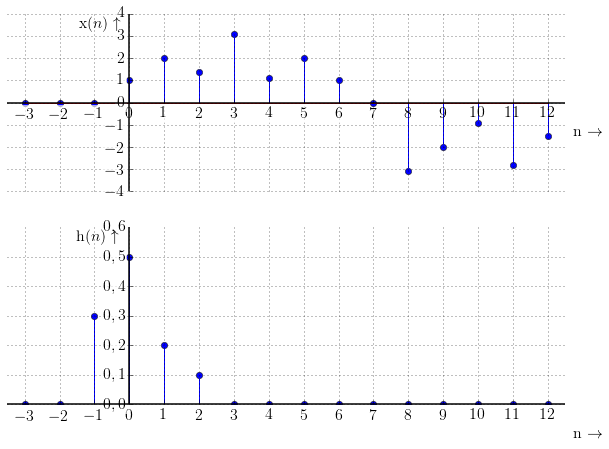
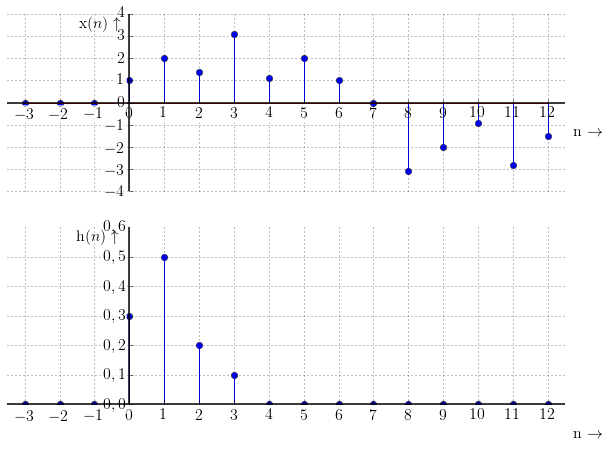
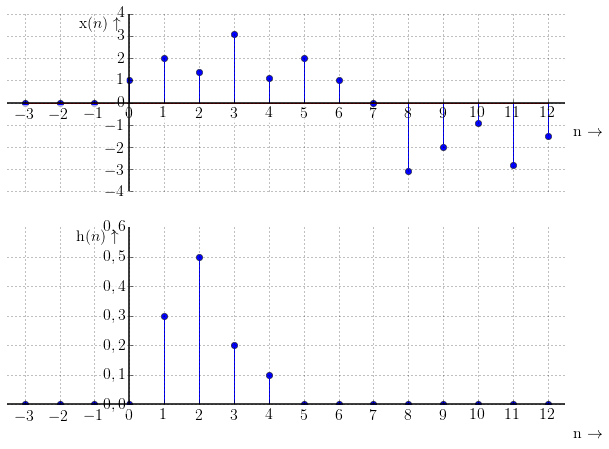
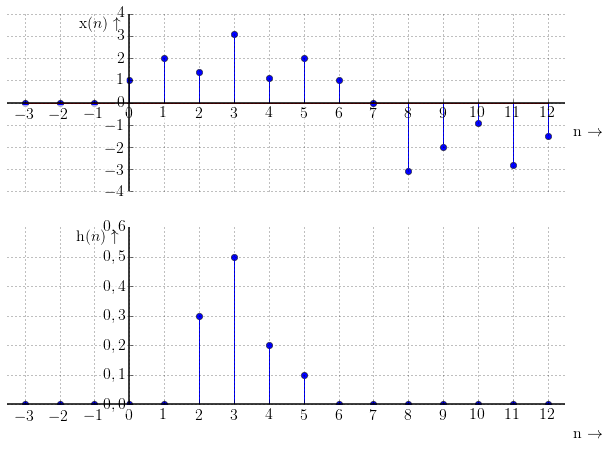
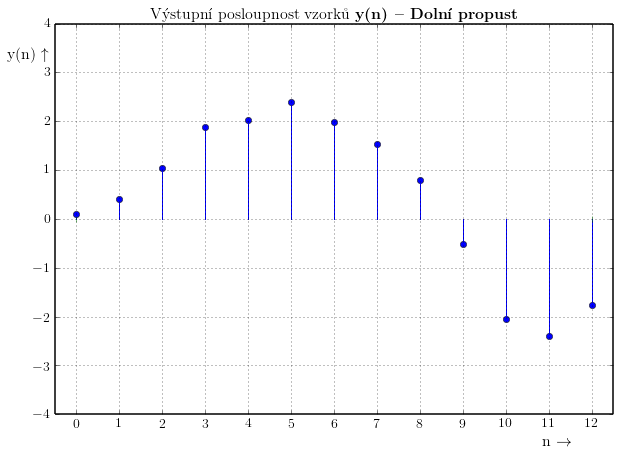
Výsledkem je posloupnost zobrazená na následujícím obrázku. Vidíme, že výstupní posloupnost připomíná funkci sinus. Filtr se tedy očividně chová jako dolní propust.

y(n)=[ 0.1 ,  0.4 ,  1.04,  1.89,  2.03,  2.39,  1.98,  1.53,  0.79, -0.52, -2.04, -2.39, -1.76]  

V této prezentaci se pokouším o prvotní přiblížení problematiky středoškolským studentům a proto zde záměrně opomíjím zpětné vazby a systémy s nekonečně dlouhou impulzní odezvou.

Python kód, který vytvořil obrázky:

Cislicovy_filtr