| Název školy: | Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 |
| Autor: | Ing. Marek Nožka |
| Anotace: | Vznik a potlačení aliasingu |
| Vzdělávací oblast: | Informační a komunikační technologie |
| Předmět: | Počítačové sítě a komunikační technika (PSK) |
| Tematická oblast: | Principy přenosu informací |
| Výsledky vzdělávání: | Žák objasňuje důvody vzniku aliasingu, důsledky aliasingu a metody předcházení aliasingu |
| Klíčová slova: | aliasing, vzorkování, digitalizace signálu |
| Druh učebního materiálu: | Online vzdělávací materiál |
| Typ vzdělávání: | Střední vzdělávání, 3. ročník, technické lyceum |
| Ověřeno: | VOŠ a SPŠE Olomouc; Třída: 3L |
| Zdroj: | Vlastní poznámky |
Bylo ukázáno, že při vzorkování dochází ke kopírování frekvenčního spektra vzorkovaného signálu s periodou ${1\over 2}f_\mathrm{s}$.
Aby nedošlo ke ztrátě dat musí být maximální frekvence vzorkovaného signálu menší než je polovina vzorkovací frekvence. Tomuto pravidlu se říká Vzorkovací theorem a matematicky ho lze zapsat jako
$$ f_\mathrm{max} \leq {f_\mathrm{s} \over 2} $$
Jinými slovy: V každé periodě vzorkovaného signálu musíme vzít alespoň dva vzorky.
V praxi se tedy vzorkovací frekvence volí dvakrát větší než je maximální požadovaná přenášená frekvence plus ještě malá rezerva. V telekomunikacích je to např. 8 kHz neboť je třeba přenášet pouze signály ve standardním telefonním pásmu (od 0,3 do 3,4 kHz). Například u záznamu na CD je to 44,1 kHz neboť průměrné zdravé lidské ucho slyší maximálně cca do 20 kHz a tudíž vzorkovací frekvence 44,1 kHz byla zvolena s určitou rezervou.
Aliasing vzniká při nedodržení vzorkovacího theoremu. To je tehdy když vzorkujeme příliš pomalu.
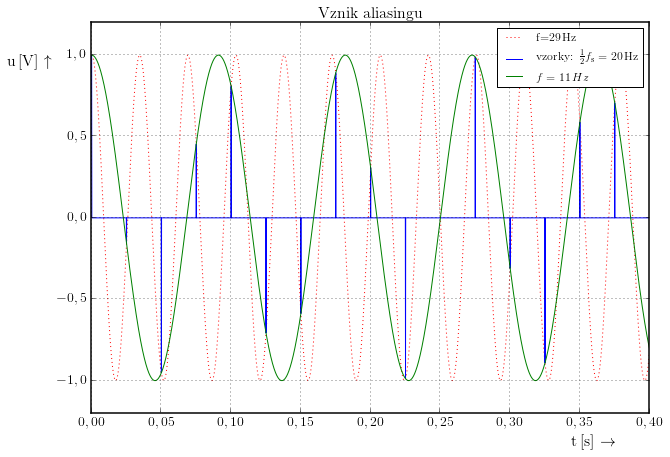
Mějme harmonický signál o frekvenci $f=29\,\mathrm{Hz}$.
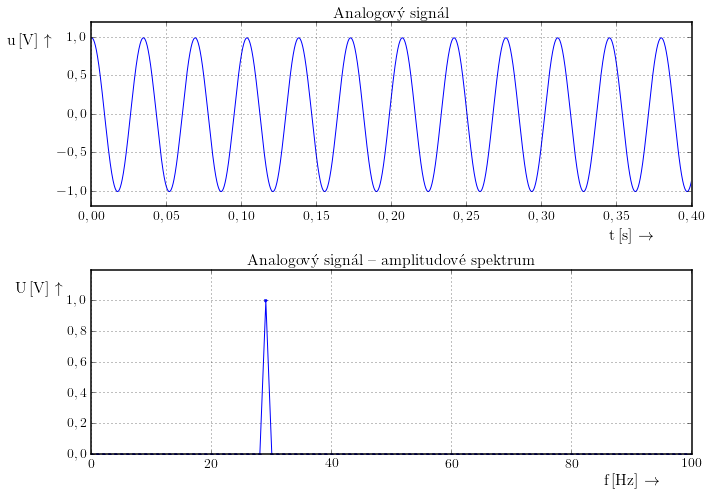
Tento signál budeme vzorkovat frekvencí $f\mathrm{s}=40\,\mathrm{Hz}$. (Touto vzorkovací frekvencí bychom měli vzorkovat signál maximálně o frekvenci $f\mathrm{max}=20\,\mathrm{Hz}$.)
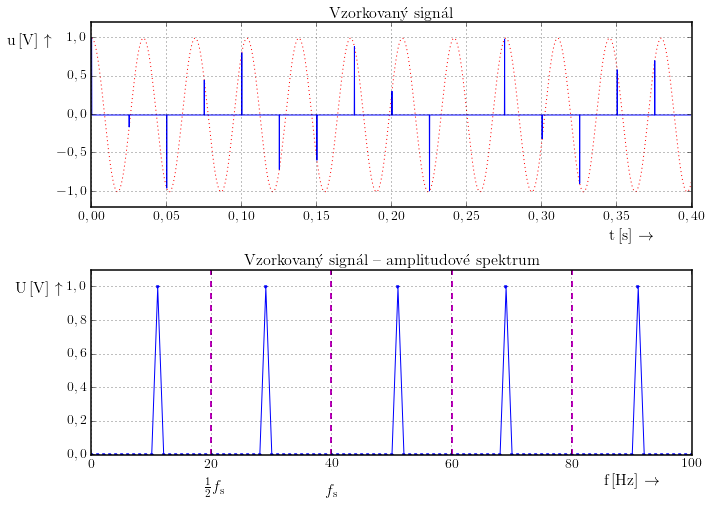
Dojde ke známému efektu: spektrum se začne kopírovat. To ale znamená, že z původní spektrální čáry na frekvenci 29 Hz je najednou spektrální čára na frekvenci 11 Hz.
Jestliže takto špatně/pomalu vzorkovaný signál přivedeme na obnovovací dolní propust o mezním kmitočtu $f_\mathrm{m} = { f_\mathrm{s} \over 2}$ stane se z původní sinusovky o frekvenci 29 Hz sinusovka o frekveci 11 Hz.
Pokud se na problém podíváme v časové oblasti, zjistíme, že při pomalém vzorkování pro jednu sadu vzorků existují dvě sinusovky.
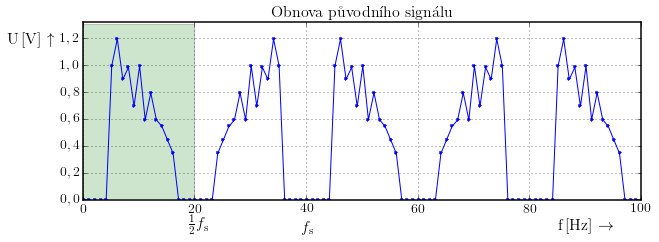
Podobný efekt můžeme pozorovat i u signálu, který obsahuje více harmonických složek: Signál jehož maximální frekvence je 16 Hz vzorkujeme frekvencí 25 Hz.
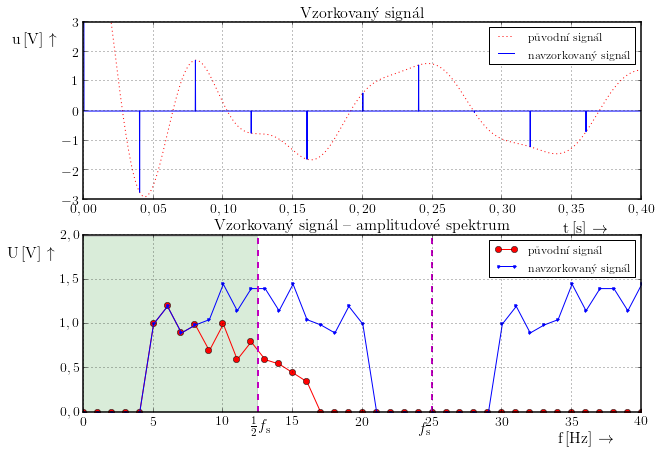
Vidíme, že začátek spektra původního a navzorkovaného signálu se překrývá ale jak se blížíme k frekvenci ${ f_\mathrm{s} \over 2}$ je spektrum porušeno aliasingem.
Antialiasingový filtr má zabránit aliasingu. To znamená, že má před vzorkováním omezit frekvenční spektrum signálu tak, aby byl splněn vzorkovací theorem. Jde opět o dolní propust s mezním kmitočtem nastaveným pod polovinu vzorkovacího kmitočtu:
$$f_\mathrm{m} \leq { f_\mathrm{s} \over 2}$$