| Název školy: | Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 |
| Autor: | Ing. Marek Nožka |
| Anotace: | Vzorkování |
| Vzdělávací oblast: | Informační a komunikační technologie |
| Předmět: | Počítačové sítě a komunikační technika (PSK) |
| Tematická oblast: | Principy přenosu informací |
| Výsledky vzdělávání: | Žák objasňuje princip vzorkování a upozorňuje na podmínky a korektního vzorkování |
| Klíčová slova: | vzorkování, digitalizace signálu |
| Druh učebního materiálu: | Online vzdělávací materiál |
| Typ vzdělávání: | Střední vzdělávání, 3. ročník, technické lyceum |
| Ověřeno: | VOŠ a SPŠE Olomouc; Třída: 3L |
| Zdroj: | Vlastní poznámky |
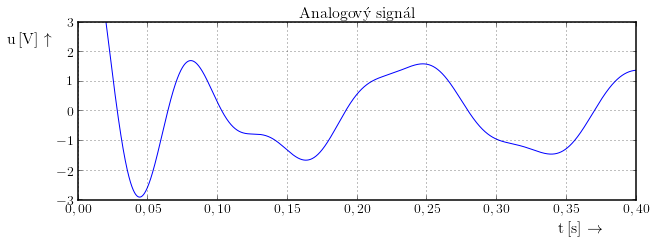
Vzorkování je proces digitalizace signálu v čase. Spočívá v odebrání vzorků ze signálu v určitých předem stanovených časových okamžicích.
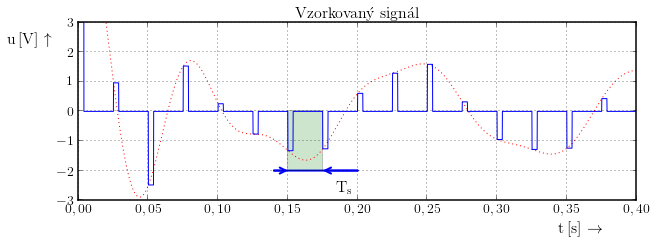
Vzdálenost jednotlivých vzorků je konstantní a označuje se jako vzorkovací perioda $T_\mathrm{s}$.
Frekvence jednotlivých vzorků je
$$ f_\mathrm{s} = \frac{1}{T_\mathrm{s}} [\mathrm{Hz, s}]$$
Index s pochází z anglického sample – vzorek.
Mějme analogový signál, jehož amplitudové frekvenční spektrum je omezené. Na obrázku vidíme analogový signál jehož frekvenční spektrum se pohybuje v rozmezí 5 Hz až 16 Hz. Tedy $f_\mathrm{min}=5\,\mathrm{Hz}$ a $f_\mathrm{max}=16\,\mathrm{Hz}$.
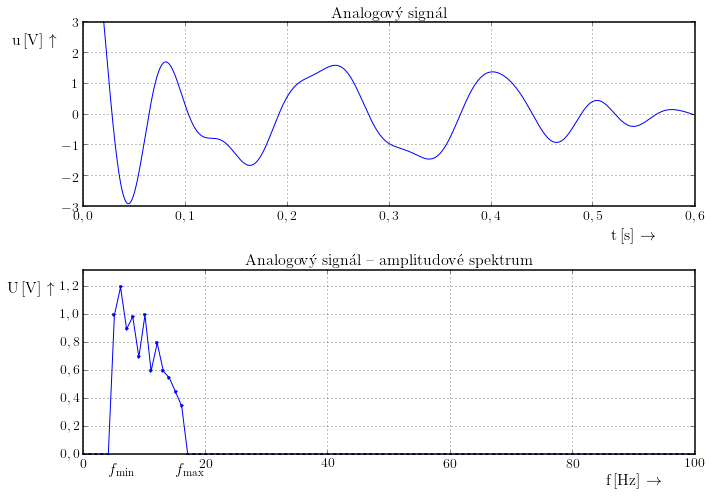
Při vzorkování dochází ke kopírování spektra do vyšších kmitočtů. Vzorek je vlastně úzký obdélníkový impulz. Víme, že spektrum obdélníkového impulzu je nekonečně široké, proto i spektrum vzorkovaného signálu musí být nekonečně široké.
Vzorkovací kmitočet je $f_\mathrm{s} = 40\,\mathrm{Hz}$. Kopírování se děje zrcadlově a osou souměrnosti je vždy polovina vzorkovacího kmitočtu a její celistvé násobky. Tedy: $\frac{1}{2}f_\mathrm{s}$, $f_\mathrm{s}$, $\frac{3}{2}f_\mathrm{s}$, $2f_\mathrm{s}$,…
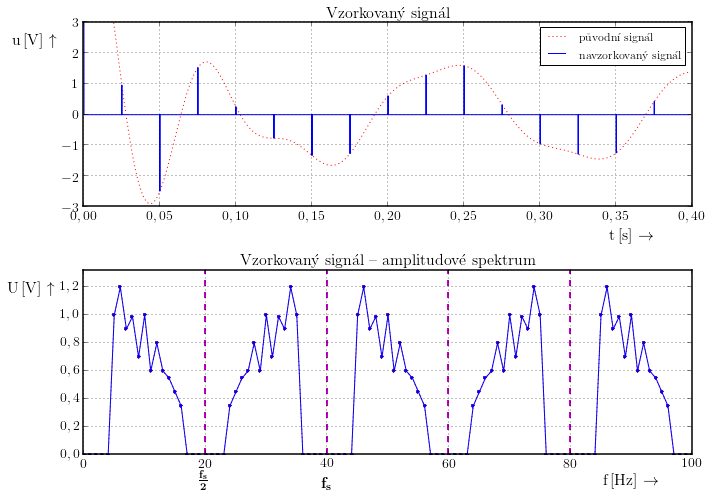
Při ideálním vzorkování by se měla šířka vzorkovacího impulzu blížit k nule. Nic ale není ideální v reálném světě toho nelze dosáhnout. Obecně lze říci, že čím je vzorkovací impulz širší tím je větší útlum na vyšších kmitočtech.
Situaci ilustrují následující obrázky. Všimněte si prosím, že změna nastává i v oblasti původního spektra a při širokém vzorkovacím impulzu tedy dochází ke ztrátě informace.
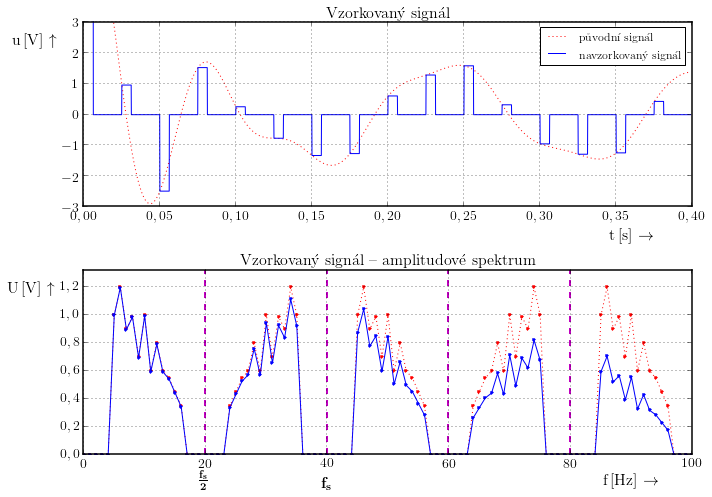
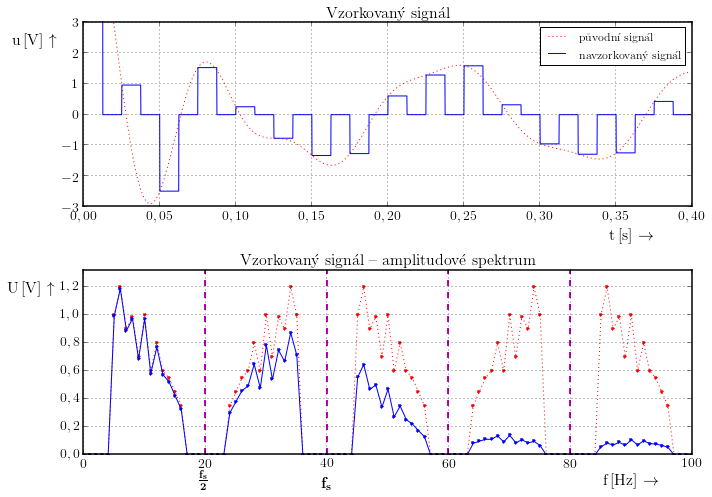
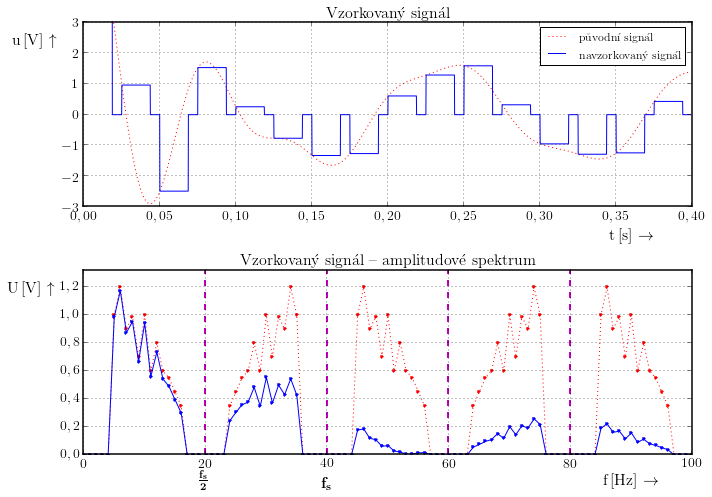
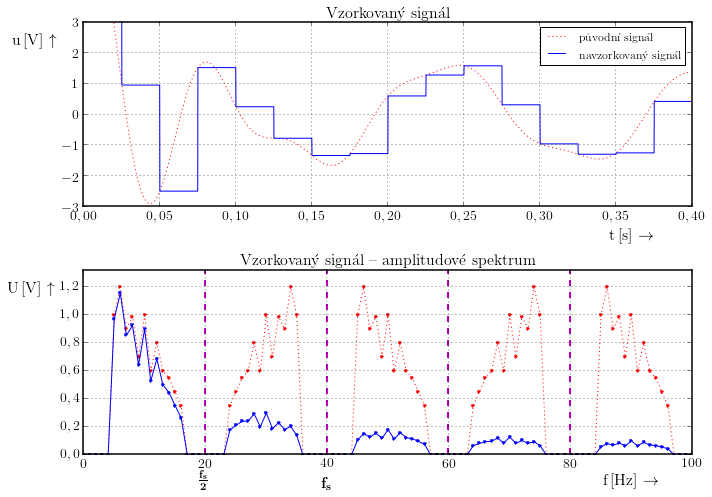
Bylo ukázáno, že při vzorkování se kopíruje spektrum s periodou $\frac{1}{2}f_\mathrm{s}$. Jestliže chceme obnovit původní signál stačí pomocí dolní propusti vybrat jen část spektra, která odpovídá původnímu signálu.
Mezní kmitočet obnovovací dolní propusti je tedy polovina vzorkovacího kmitočtu.
$$f_\mathrm{m} = { f_\mathrm{s} \over 2}$$