

| Název školy: | Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 |
| Autor: | Ing. Marek Nožka |
| Anotace: | Frekvenční modulace |
| Vzdělávací oblast: | Informační a komunikační technologie |
| Předmět: | Počítačové sítě a komunikační technika (PSK) |
| Tematická oblast: | Principy přenosu informací |
| Výsledky vzdělávání: | Žák objasní princip přenosu dat pomocí frekvenční modulace, srovnává FM a AM |
| Klíčová slova: | frekvenční modulace, přenos dat |
| Druh učebního materiálu: | Online vzdělávací materiál |
| Typ vzdělávání: | Střední vzdělávání, 3. ročník, technické lyceum |
| Ověřeno: | VOŠ a SPŠE Olomouc; Třída: 3L |
| Zdroj: | Vlastní poznámky |
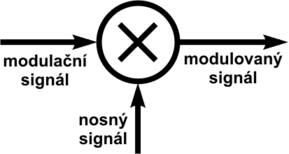
Do modulátoru vstupují signály, kterým říkáme modulační a nosný. Modulační signál je ten, který chceme přenést a k jeho přenesení používáme nosný signál. Z modulátoru vystupuje modulovaný signál.
Nosný signál je vždy harmonický a lze ho popsat matematickou rovnicí:
$$ u_\mathrm{c} = U_{\mathrm{c}} \sin(2 \mathrm{\pi} f t + \varphi) $$
Frekvenční modulace spočívá v ovlivňování okamžité frekvence nosné vlny $f_\rm{c}$ okamžitou hodnotou modulačního signálu.
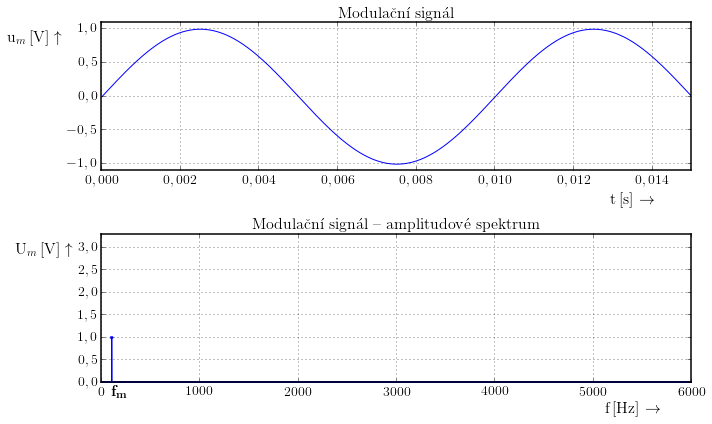
Na obrázku vidíme harmonický modulační signál o frekvenci $f_\rm{m}$=100 Hz a jeho amplitudové spektrum.
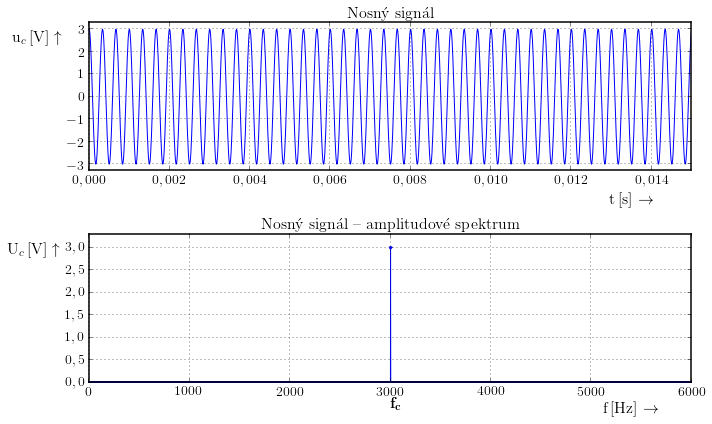
Nosný signál má (mnohem) větší frekvenci, než signál modulační. Na obrázku je nosná vlna o frekvenci $f_\rm{c}$=3 kHz a její amplitudové spektrum.
Při frekvenční modulaci se mění okamžitá frekvence v rytmu modulačního signálu. To se projeví jako "zhušťování" a "zřeďování" modulovaného signálu. Situaci ilustruje následující obrázek.
Zvláště si prosím povšimněte, co se stalo s amplitudovým frekvenčním spektrem. Velikost harmonické složky na kmitočtu $f_{\mathrm{c}}$ je mnohem menší než původně a kolem kmitočtu $f_{\mathrm{c}}$ vyrostlo velké množství nových harmonický složek. Vzdálenost jednotlivých spektrálních čar je $f_{\mathrm{c}}$.
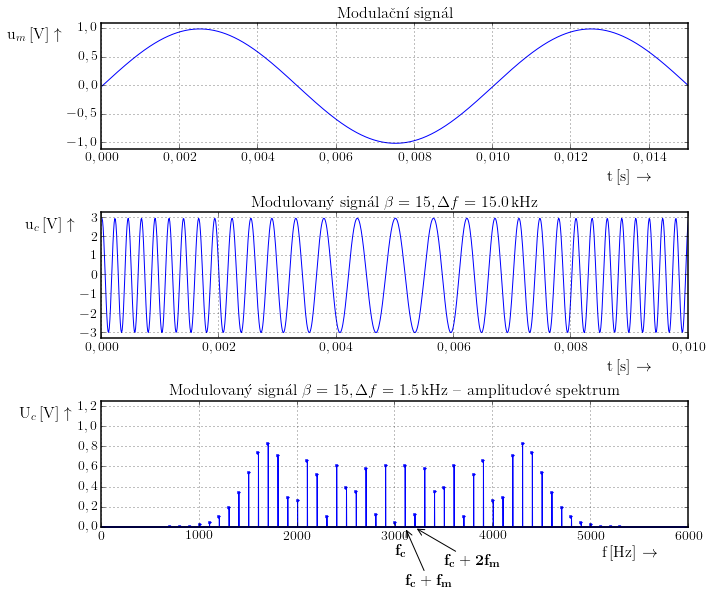
Jak Kmitočtový zdvih a index modulace ovlivňují výsledný modulovaný signál je vidět na následujícím obrázku. Menší frekvenční zdvih respektive menší index modulace má za následek rychlejší pokles harmonických složek kolem nosného kmitočtu. Tím klesá i šířka pásma.
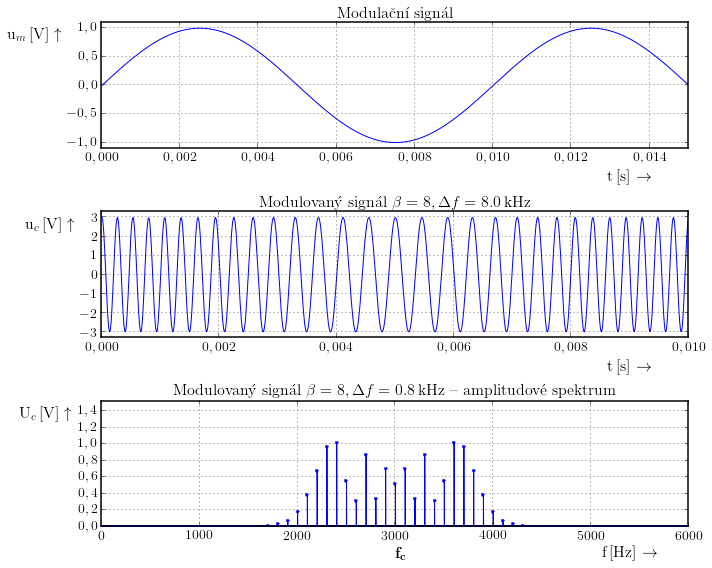
Šířka pásma udává jak velkou frekvenční oblast zaujme jedna stanice přenášená pomocí frekvenční modulace. U frekvenční modulace je šířka pásma teoreticky nekonečně velká, protože při jejím matematickém popisu zjistíme, že jednotlivých harmonických složek je nekonečně mnoho.
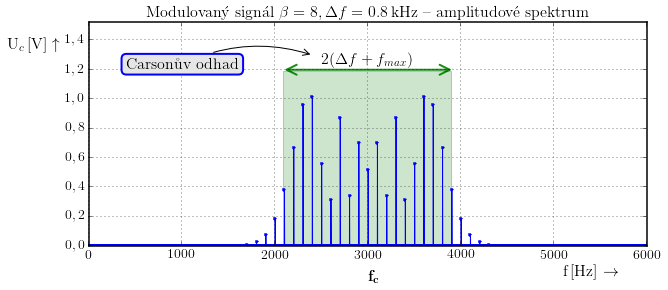
Při pohledu na amplitudové spektrum frekvenční modulace je ale jasné, že velikost některých harmonických složek je tak malá, že je můžeme zanedbat. Proto se mluví o praktické šířce pásma, která se dá vypočítat pomocí tzv. Carsonova odhadu. Tento vztah je empirický a platí pro index FM v rozsahu 1 až 20.
$$ B \ 2(\Delta f+f_{max}); ~~ [Hz; Hz, Hz]; ~~ \beta \in (1,20) $$
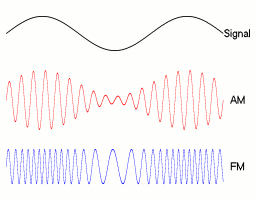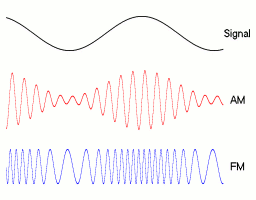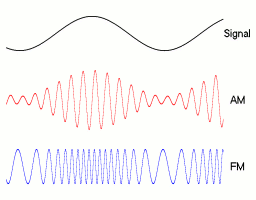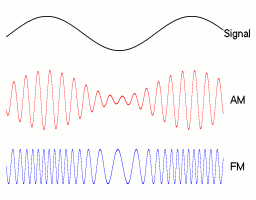
Amplitudová modulace vyniká svou relativně malou šířkou pásma. Na druhou stranu má ale velice malou odolnost proti rušení. U frekvenční modulace je tomu naopak. FM má velice dobrou odolnost vůči rušení, ale zato také velkou šířku pásma.
Amplitudová modulace se tedy dá použít i v nižších frekvenčních pásmech jakou jsou například střední vlny. Maximální modulační frekvence je zde omezena na $f_{\mathrm{max}}=4{,}5\,\mathrm{kHz}$, šířka pásma je tedy $B=9\,\mathrm{kHz}$
Frekvenční modulace se pro svou větší šířku pásma používá až ve vyšších frekvenčních pásmech. Například u radiového vysílání v pásmu velmi krátkých vln se používá frekvenční zdvih $\Delta f=75\,\mathrm{kHz}$ a modulační signál je omezen na $f_{\mathrm{max}}=15\,\mathrm{kHz}$.